PERTEMUAN 11 NORMALITAS

                                NORMALITAS

 Pengertian Uji Normalitas 

      Uji Normalitas data adalah bentuk pengujian tentang kenormalan distribusi data. 

Tujuan dari uji ini adalahuntuk mengetahui apakah data yang terambil merupakan data 

terdistribusi normal atau bukan. Maksud dari data berdistribusi normal adalah data akan 

mengikuti bentuk distribusi normal di mana data memusat pada nilai rata – rata dan 

median. Rumus yang digunakan adalah rumus kai kuadrat ( chi – kuadrat ).Prosedur 

Pengujian Normalitas data.

     Prosedur pengujian normalitas data :

1.Merumuskan formula hipotesis

Ho : Data berdistribusi normal

Ha : Data tidak berdistribusi normal

2. Menentukan taraf nyata (a)

Untuk mendapatkan nilai chi-square tabel

dk = k – 3

dk = Derajat kebebasan

k = banyak kelas interval

3. Menentukan Nilai Uji Statistik

Keterangan :

Oi = frekuensi hasil pengamatan pada klasifikasi ke-i

Ei = Frekuensi yang diharapkan pada klasifikasi ke-i

4. Menentukan Kriteria Pengujian Hipotesis

5. Memberikan kesimpulan

     Syarat Uji Chi-Square dalam Uji Normalitas

Persyaratan Metode Chi Square (Uji Goodness of fit Distribusi Normal)

a. Data tersusun berkelompok atau dikelompokkan dalam tabel distribusi frekuensi.

b. Cocok untuk data dengan banyaknya angka besar ( n > 30 )

c. Setiap sel harus terisi, yang kurang dari 5 digabungkan.

Signifikansi:

Signifikansi uji, nilai X2 hitung dibandingkan dengan X2 tabel (Chi-Square).

Jika nilai X2 hitung < nilai X2 tabel, maka Ho diterima ; Ha ditolak.

Jika nilai X2 hitung > nilai X2 tabel, maka maka Ho ditolak ; Ha diterima.

CONTOH SOAL 

Contoh:
Diambil Tinggi Badan Mahasiswa Di Suatu Perguruan Tinggi Tahun 2010

Selidikilah dengan α = 5%, apakah data tersebut di atas berdistribusi normal ? (Mean = 157.8; Standar deviasi = 8.09)
Penyelesaian :
1. Hipotesis :

Ho : Populasi tinggi badan mahasiswa berdistribusi normal
H1 : Populasi tinggi badan mahasiswa tidak berdistribusi normal

2. Nilai α

Nilai α = level signifikansi = 5% = 0,05

3. Rumus Statistik penguji

Luasan pi dihitung dari batasan proporsi hasil tranformasi Z yang dikonfirmasikan dengan tabel distribusi normal atau tabel z.

4. Derajat Bebas

Df = ( k – 3 ) = ( 5 – 3 ) = 2

5. Nilai tabel

Nilai tabel X2 ; α = 0,05 ; df = 2 ; = 5,991. 

6. Daerah penolakan

Menggunakan gambar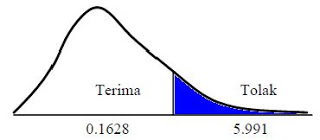

Menggunakan rumus:   |0,427 | < |5,991| ; Keputusan hipotesis: berarti Ho diterima, Ha ditolak

7. Kesimpulan:  Populasi tinggi badan mahasiswa berdistribusi normal α = 0,05.

TUGAS UJI NORMALISASI

1. Ujilah data di bawah ini apakah berdistribusi normal atau tidak

jawab: 

1). Hipotesis 

     H0: Berdistribusi Normal

     H1: Tidak Berdistribusi Normal

2). Nilai a

      Nilai a = Level Signifikan =  5% = 0.05

3). Rumus Statistik Terpuji

      

4). Derajat Bebas

     Df = (k Panjang Kelas)-3) = (10-3) = 7

5). Nilai Tabel 

     Nilai tabel x Pangkat 2: a = 0.05, df = 7 = 14,067 tabel x pangkat 2 lampiran

6). Daerah penolakan 

     Menggunakan Rumus

     -176,2 < 14,067: H0 diterima, Ha ditolak

7). Kesimpulan

     Hasil uji data diatas menghasilkan Distribusi Normal

                                                                                                                Della Anastiya Putri

                                                                                                                   (181011401023)